Circle Difference Between 2 Pictures Nds Game
Suppose there is a circle. There are n petrol pumps on that circle. You are given two sets of data.
- The amount of petrol that every petrol pump has.
- Distance from that petrol pump to the next petrol pump.
Calculate the first point from where a truck will be able to complete the circle (The truck will stop at each petrol pump and it has infinite capacity). Expected time complexity is O(n). Assume for 1-litre petrol, the truck can go 1 unit of distance.
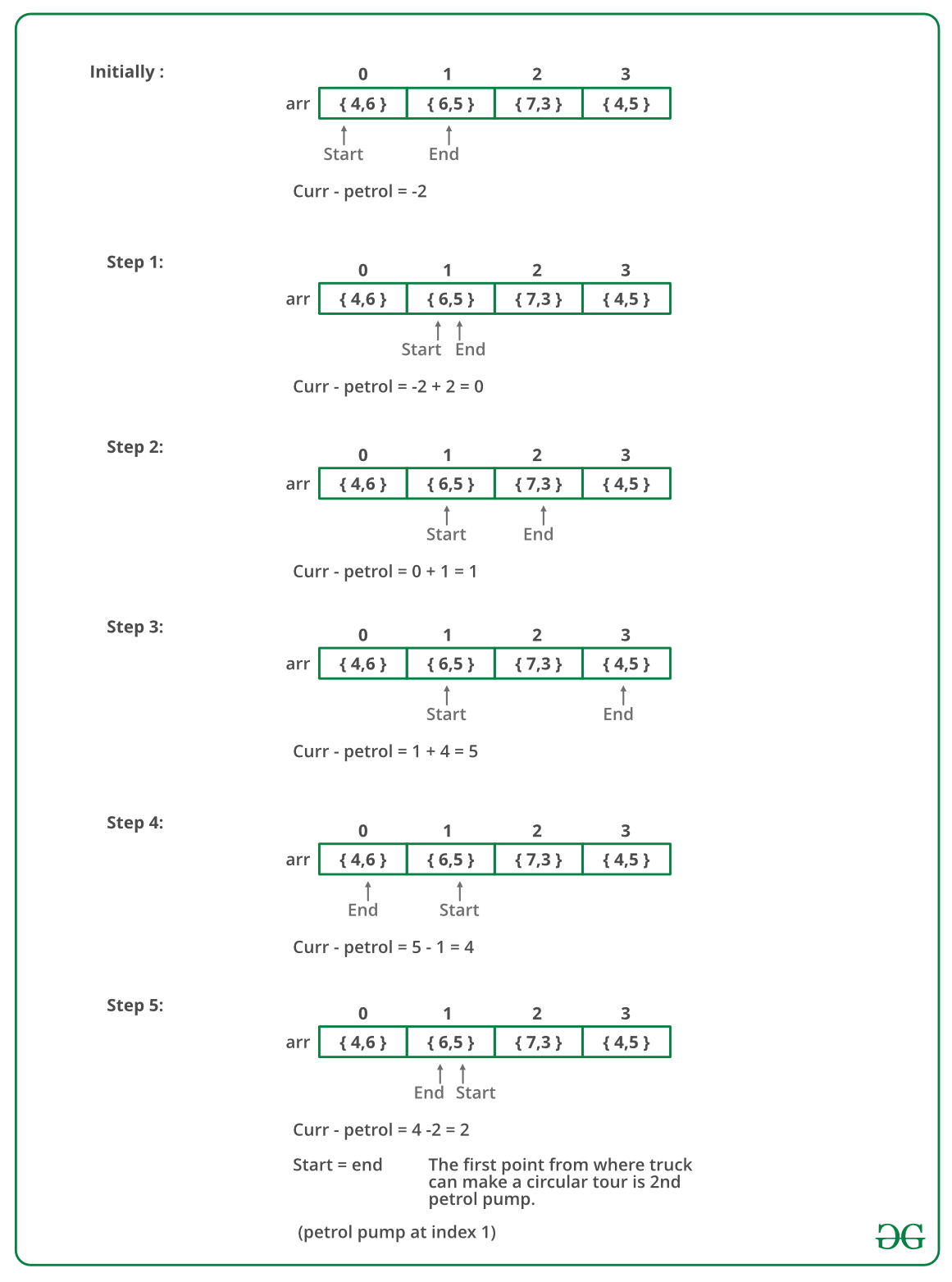
For example, let there be 4 petrol pumps with amount of petrol and distance to next petrol pump value pairs as {4, 6}, {6, 5}, {7, 3} and {4, 5}. The first point from where the truck can make a circular tour is 2nd petrol pump. Output should be "start = 1" (index of 2nd petrol pump).
Become a success story instead of just reading about them. Prepare for coding interviews at Amazon and other top product-based companies with our Amazon Test Series. Includes topic-wise practice questions on all important DSA topics along with 10 practice contests of 2 hours each. Designed by industry experts that will surely help you practice and sharpen your programming skills. Wait no more, start your preparation today!
A Simple Solution is to consider every petrol pumps as a starting point and see if there is a possible tour. If we find a starting point with a feasible solution, we return that starting point. The worst case time complexity of this solution is O(n^2).
An efficient approach is to use a Queue to store the current tour. We first enqueue first petrol pump to the queue, we keep enqueueing petrol pumps till we either complete the tour, or the current amount of petrol becomes negative. If the amount becomes negative, then we keep dequeuing petrol pumps until the queue becomes empty.
Instead of creating a separate queue, we use the given array itself as a queue. We maintain two index variables start and end that represent the rear and front of the queue.
Below image is a dry run of the above approach:
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump
{
public :
int petrol;
int distance;
};
int printTour(petrolPump arr[], int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1) % n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1) % n;
}
return start;
}
int main()
{
petrolPump arr[] = {{6, 4}, {3, 6}, {7, 3}};
int n = sizeof (arr)/ sizeof (arr[0]);
int start = printTour(arr, n);
(start == -1)? cout<< "No solution" : cout<< "Start = " <<start;
return 0;
}
C
#include <stdio.h>
struct petrolPump
{
int petrol;
int distance;
};
int printTour( struct petrolPump arr[], int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1)%n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1)%n;
}
return start;
}
int main()
{
struct petrolPump arr[] = {{6, 4}, {3, 6}, {7, 3}};
int n = sizeof (arr)/ sizeof (arr[0]);
int start = printTour(arr, n);
(start == -1)? printf ( "No solution" ): printf ( "Start = %d" , start);
return 0;
}
Java
public class Petrol
{
static class petrolPump
{
int petrol;
int distance;
public petrolPump( int petrol, int distance)
{
this .petrol = petrol;
this .distance = distance;
}
}
static int printTour(petrolPump arr[], int n)
{
int start = 0 ;
int end = 1 ;
int curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0 )
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1 ) % n;
if (start == 0 )
return - 1 ;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1 )%n;
}
return start;
}
public static void main(String[] args)
{
petrolPump[] arr = { new petrolPump( 6 , 4 ),
new petrolPump( 3 , 6 ),
new petrolPump( 7 , 3 )};
int start = printTour(arr, arr.length);
System.out.println(start == - 1 ? "No Solution" : "Start = " + start);
}
}
Python
def printTour(arr,n):
start = 0
s = 0
d = 0
for i in range (n):
s + = arr[i][ 0 ] - arr[i][ 1 ]
if s < 0 :
start = i + 1
d + = s
s = 0
return start if (s + d)> = 0 else - 1
arr = [[ 6 , 4 ], [ 3 , 6 ], [ 7 , 3 ]]
start = printTour(arr, 3 )
if start = = - 1 :
print ( "No Solution Possible !!!" )
else :
print ( "start = {}" . format (start))
C#
using System;
class GFG
{
public class petrolPump
{
public int petrol;
public int distance;
public petrolPump( int petrol,
int distance)
{
this .petrol = petrol;
this .distance = distance;
}
}
public static int printTour(petrolPump[] arr,
int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol -
arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol -
arr[start].distance;
start = (start + 1) % n;
if (start == 0)
{
return -1;
}
}
curr_petrol += arr[end].petrol -
arr[end].distance;
end = (end + 1) % n;
}
return start;
}
public static void Main( string [] args)
{
petrolPump[] arr = new petrolPump[]
{
new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3)
};
int start = printTour(arr, arr.Length);
Console.WriteLine(start == -1 ? "No Solution" :
"Start = " + start);
}
}
Javascript
<script>
class petrolPump {
constructor(petrol, distance) {
this .petrol = petrol;
this .distance = distance;
}
};
const printTour = (arr, n) => {
let start = 0;
let end = 1;
let curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0) {
while (curr_petrol < 0 && start != end) {
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1) % n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1) % n;
}
return start;
}
let arr = [ new petrolPump(6, 4), new petrolPump(3, 6), new petrolPump(7, 3)];
let n = arr.length;
let start = printTour(arr, n);
(start == -1) ? document.write( "No solution" ) : document.write(`Start = ${start}`);
</script>
Output:
start = 2
Time Complexity: We are visiting each petrol pump exactly once, therefore the time complexity is O(n)
Auxiliary Space: O(1)
Another efficient solution can be to find out the first petrol pump where the amount of petrol is greater than or equal to the distance to be covered to reach the next petrol pump. Now we mark that petrol pump as start and now we check whether we can finish the journey towards the end point. If in the middle, at any petrol pump, the amount of petrol is less than the distance to be covered to reach the next petrol pump, then we can say we cannot complete the circular tour from start. We again try to find out the next point from where we can start our journey i.e. the next petrol pump where the amount of petrol is greater than or equal to the distance to be covered and we mark it as start. We need not look at any petrol pump in between the initial petrol pump marked as start and the new start as we know that we cannot complete the journey if we start from any middle petrol pump because eventually we will arrive at a point where amount of petrol is less than the distance. Now we repeat the process until we reach the last petrol pump and update our start as and when required. After we reach our last petrol pump, we try to reach our first petrol pump from the last and let's say we have a remaining amount of petrol as curr_petrol. Now we again start traveling from the first petrol pump and take the advantage of our curr_petrol and try to reach the start. If we can reach the start, then we may conclude that start can be our starting point.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump {
public :
int petrol;
int distance;
};
int printTour(petrolPump arr[], int n)
{
int start;
for ( int i = 0; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
break ;
}
}
int curr_petrol = 0;
int i;
for (i = start; i < n;) {
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break ;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for ( int j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
int main()
{
petrolPump arr[] = { { 6, 4 }, { 3, 6 }, { 7, 3 } };
int n = sizeof (arr) / sizeof (arr[0]);
int start = printTour(arr, n);
(start == -1) ? cout << "No solution"
: cout << "Start = " << start;
return 0;
}
Javascript
<script>
class petrolPump {
constructor(petrol, distance) {
this .petrol = petrol;
this .distance = distance;
}
};
const printTour = (arr, n) => {
let start;
for (let i = 0; i < n; i++)
{
if (arr[i].petrol >= arr[i].distance) {
start = i;
break ;
}
}
let curr_petrol = 0;
let i;
for (i = start; i < n;)
{
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break ;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (let j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
let arr = [ new petrolPump(6, 4), new petrolPump(3, 6), new petrolPump(7, 3)];
let n = arr.length;
let start = printTour(arr, n);
(start == -1) ? document.write( "No solution" ) : document.write(`Start = ${start}`);
</script>
Output:
start = 2
Time Complexity: O(n)
Auxiliary Space: O(1)
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Circle Difference Between 2 Pictures Nds Game
Source: https://www.geeksforgeeks.org/find-a-tour-that-visits-all-stations/
0 Response to "Circle Difference Between 2 Pictures Nds Game"
Post a Comment